IFA Index Calculator
Retirement Calculator
Target Date Calculator
Retirement Income
College Planning
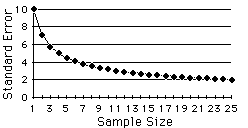
T-Statistic Calculator
401(k) Calculator
Net Worth
Net Income
Roth IRA Conversion
Fee Calculator
Multi Funds Calculator
MENU
Home
Risk CapacitySurvey
Wealth Management
Retirement Plans
Institutional
Taxes
Financial Calculators ▾
Open an Account
Connect with an Advisor
IFA App
Videos ▾
Articles
Charts
Investor Education ▾
IndexPortfolios ▾
FundOptions
Resources▾
About Us ▾
Store
GaltonBoard
Petition
Back-testing Disclosures
Index Descriptions
Glossary
Form CRS
Risk & Return
Matching People With PortfoliosRisk and Return
Figure 1(permalink)
The most common risk measure is standard deviation — a statistic measurement of volatility that tells you how tightly the various annual returns are clustered around the average. When the annual returns are tightly bunched together the standard deviation is small and the bell-shaped curve is narrow. When the annual returns are spread apart and the bell curve is relatively flat, it tells you that you have a relatively large standard deviation.
The combination of the average and the standard deviation characterize various bell curve shapes, and those shapes represent the risk and return of the Index Portfolio. Figure 2 shows you graphically what a standard deviation represents.
Figure 2(permalink)
One standard deviation away from the average in both directions on the horizontal axis (the yellow area on the graph) accounts for somewhere around 68 percent of the annual returns in the time period. Two standard deviations away from the mean (the yellow and green areas) account for roughly 95 percent of the annual returns. And three standard deviations (the yellow, green and orange areas) account for about 99 percent of the annual returns.
Standard Error
The standard error of the mean indicates the degree of uncertainty in calculating an estimate from a sample, like a series of returns data. A standard error can be calculated from the standard deviation by dividing the standard deviation by a square root of the sample size. So with only 3 years of returns data on the S&P 500, the error in the average return is 2.6 times larger than having 20 years of data.
Risk and Return Tables
Figure 3(permalink)
Figure 4(permalink)
Figure 5(permalink)
Figure 6(permalink)
Figure 7(permalink)
More About Our Portfolios
To achieve optimal results, investors need to match their Risk Capacity with a specific risk exposure aligned to one of our 100 Portfolios.
What's your Risk Capacity?
Calculating risk capacity is the first step to deciding which portfolio will generate optimal returns for each investor.
Each investor has a unique risk capacity and can be identified by a risk capacity score — a measure of
how much risk one can manage.
HomeTaxesAbout Us
888-643-3133
Contact Us
Newsletter Subscribe
eMoney
IFA Apps
Index Funds Book on Kindle
Index Funds Audiobook
Careers
Facebook
X
LinkedIn
InstagramVideos
YoutubeGlossary
TermsDisclosuresIndex DescriptionsForm CRS The data provided in charts referring to IFA Index Portfolios is hypothetical back-tested performance and is not actual client performance. Performance data for the IFA Index Portfolios is shown net of IFA's highest advisory fee and the underlying mutual fund expenses. IFA Indexes when shown individually do not reflect a deduction of advisory fees. None of the data reflects trading costs or taxes, which would have lowered performance by these costs. See more important disclosures at ifabt.com.
© 1999-2025 Index Fund Advisors, Inc. All Rights Reserved | 19200 Von Karman Ave. Suite 150 Irvine, CA 92612 | 888-643-3133