In the field of finance, a key element to study is how much market risk investors are undertaking in owning a portfolio of globally diverse securities. 

A measure IFA's portfolio management and research group uses is standard deviation, which represents the risk associated with a security (i.e., stocks or bonds) -- or, the risk of a portfolio of securities (including actively managed mutual funds, index mutual funds or exchange-traded funds).

Risk is an important factor in determining how to efficiently manage investments because it determines the variation in returns on the asset and/or portfolio. Standard deviation gives investors a mathematical basis for investment decisions (the basis for mean-variance optimization).

The overall concept of risk is that as it increases, the expected return on the asset should increase as a result of the risk premium earned. In other words, investors should not expect a higher return on an investment without that investment having a higher degree of risk, or uncertainty of those returns.

When evaluating portfolios, investors should always estimate both the expected return and the uncertainty of that return. Standard deviation provides a quantified estimate of the uncertainty of those future returns, the average of which is the expected return. The graphic below ("Why Diversify? Stocks vs Indexes and IFA Index Portfolios") illustrates this point.

For example, let's assume an investor had to choose between two stocks and an S&P 500 Index Fund.

1) International Business Machines Corp. (IBM)
2) Proctor & Gamble (PG)
3) S&P 500 Index Fund

Neither stock is a good choice because an S&P 500 index fund over the period shown in this graphic earned a similar annualized return with a lower volatiliy (i.e., uncertainty as measured by standard deviation) because of the diversification benefit of 500 stocks versus one stock. Quantitatively, this makes the S&P 500 Index fund the statistically preferred investment over individual stocks.

You can see from the graph below that even stocks that had higher returns than the S&P 500 required higher levels of risk. If you drew a diagonal line along the IFA Index Portfolios, you can see that all stocks but WalMart fell below the line.

If you diversified from simply holding a passively managed S&P 500 index fund into other global markets and small value index fund -- like Index Portfolio 100  -- the annualized return in this same period was higher, with a similar standard deviation, making Index Portfolio 100 the statistically preferred investment over the S&P 500 and anything else that we can find.

An important caveat exists, however. Please note that investors must first determine their risk capacity before making investment choices. Then, they can determine which investments have the highest expected return for the standard deviation that is right for them. (In our view, the maximum risk exposure for any investor should be Index Portfolio 100.)

To determine the standard deviation of a certain stock or index, start by calculating the average return (or arithmetic mean) of the security over a given number of periods, like 20 years or more. For each year, subtract the average return from the actual return for that year, which will give you the "variances." Then, square the variance in each period.

The larger the variance in a period, the greater risk the security carries. Calculate the average of the squared variances and then calculate the square root of this average variance. This will get you the standard deviation of the investment in question.

Another point to keep in mind: The arithmetic mean is used to calculate the standard deviation. But when comparing returns of stocks or indexes, it is customary to use the annualized average return, not the arithmetic mean return. 

Volatility (or standard deviation) relative to the market, also known as beta, is one way to look at risk. There are three risk factors that have explained 95% of the variability of stock market returns, dating back to 1929. (The 23-page academic study that supports this can be found here.)

According to a landmark study by Eugene Fama and Kenneth French in 1992, the three factors that explain 95% of the variability of stock market returns are Beta (Market Risk); Market Capitalization (Size Risk); and Value (high Book-to-Market Risk).

Under such a model, small value stocks have the highest expected return. Non-U.S. and emerging markets provide opportunities for the diversification of more small and even more value-tilted stocks as well as additional country risks, which all results in higher cost of capital for those firms and higher expected returns for investors.

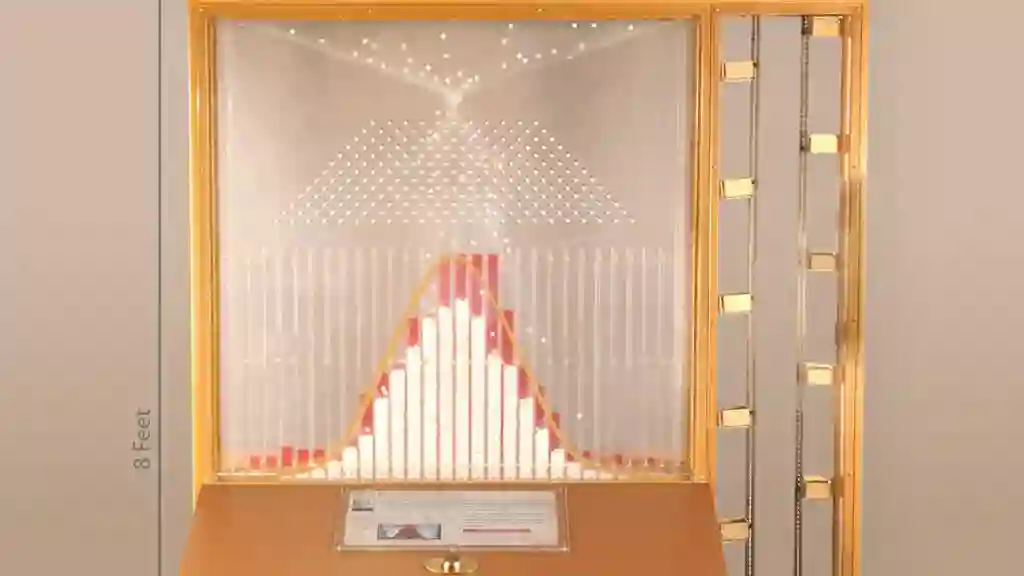
An investment like Index Portfolio 100 is highly volatile. The first chart below shows the annual returns during an extended period in the top graph. A histogram based on the average return and standard deviation is illustrated by the bottom graph.

Both graphics are interactive in that you can toggle between different IFA Index Portfolios with various levels of stocks and bonds. For example, you can click on Index Portfolio 50, a more moderate risk portfolio with 50% stocks and 50% bonds, to compare risk-return tradeoffs.

At the other end of the spectrum, you might find it interesting to look at such patterns for Index Portfolio 10, which is 90% comprised of bond funds. Note the lack of volatility over these extended periods on the top graph and the narrow distribution of the bell curve on the bottom graph.

Another important statistical concept is the standard error of the mean, which indicates the degree of uncertainty in calculating an estimate from a sample -- like a series of returns data.

A standard error can be calculated from the standard deviation by dividing the standard deviation by a square root of n (with n representing the number of years measured). So with only three years of returns data on the S&P 500, the error in the average return is 2.6 times larger than having 20 years of data. 

---

This is not to be construed as an offer, solicitation, recommendation, or endorsement of any particular security, product or service. There is no guarantee investment strategies will be successful. Investing involves risks, including possible loss of principal. Performance may contain both live and back-tested data. Data is provided for illustrative purposes only, it does not represent actual performance of any client portfolio or account and it should not be interpreted as an indication of such performance. IFA Index Portfolios are recommended based on time horizon and risk tolerance. Take the IFA Risk Capacity Survey (www.ifa.com/survey) to determine which portfolio captures the right mix of stock and bond funds best suited to you. For more information about Index Fund Advisors, Inc, please review our brochure at https://www.adviserinfo.sec.gov/ or visit www.ifa.com.