In a casino, it's not uncommon to see purportedly random occurrences that actually hint at being not so inexplicable — or, in mathmatical terms, non-random events.

Perhaps the roulette wheel came up red seven times in a row and your reaction was to place a large bet on black because black was "due." Maybe such repetition of seemingly random patterns caused you to bet on red because that color looked "hot."

If so, then you fell into a trap known as "the gambler's fallacy." In behavioral science terms, such a fallacy is the result of mistakingly thinking that the outcome of a random event is influenced by outcomes of prior circumstances, when in reality, each occurrence stands on its own.

Unfortunately, the gambler's fallacy too often leads to the gambler's ruin. A classic case was exposed in the mid-2000s when several betters made a very public case that the number 53 was due to come up in a national lottery held at the time in Italy. More than $3 billion worth of euros were reportedly bet on such a pick, which proponents credited to various statistical manipulations and data-crunching exercises.

The number 53 became a sort of national obsession, according to a BBC report at the time. It eventually did land on that number, but experts pointed out it came only after an abnormally long time. In the meantime, a woman reportedly drowned herself at sea after betting her family's savings on the number.  Several other tragic cases were detailed in the media during a two-year span. 

Lack of Understanding

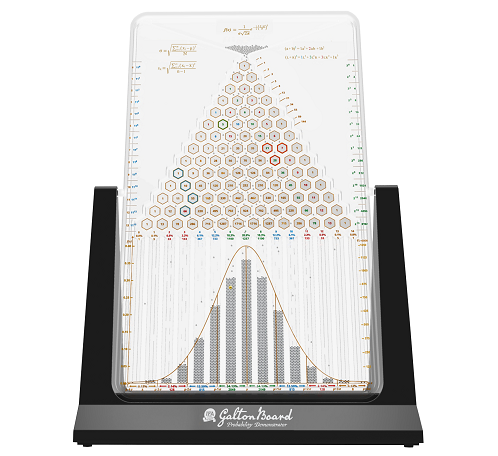
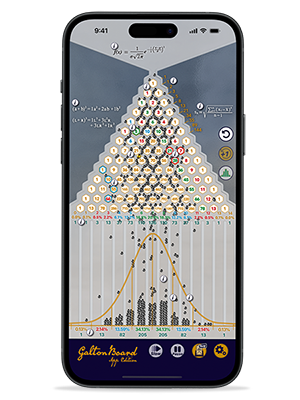
The tragic consequences of these bets could so easily have been avoided, especially in light of the fact that these bets resulted from a misunderstanding of "The Law of Large Numbers." This statistical rule states that the average of the results obtained from a large number of trials should be close to the expected value — and will tend to become closer as more trials are performed.

The key point of this mathematical law is that the observed proportion of trials meeting a given criterion — e.g., coin flips coming up heads — converges on its expected value as the number of trials increases. This is not the same thing as saying that the number of 'heads' converges immediately on 50% of the number of flips. 

For example, if a coin is flipped 100 times, it would not be unusual to have 55 'heads' and 45 'tails.' (This, of course, would represent a 'one standard deviation' event, equating to a 32% probability of occurrence).

However, if the coin is flipped 1,000 times, the chances of having 550 'heads' and 450 'tails' are quite remote. (This would represent a 'three standard deviation' event and equate to a 0.3% probability of occurrence). If this event were to happen, it does not mean that in the next 1,000 flips we'd expect more 'tails' — as opposed to 'heads' — would come up to even the score. If we simply had the expected number of 500 'heads,' then the overall percentage of heads in the 2,000 flips would drop to 52.5%, in accordance with what we would expect from the Law of Large Numbers.

Another common fallacy tied to the law of large numbers: If something happens more frequently than normal during a given period, it will happen less frequently in the future (or vice versa). This belief often arises out of an overconfidence in the law of small numbers — i.e., the erroneous belief that small samples are representative of the larger population. 

According to the fallacy, 'streaks' must eventually even out in order to be representative. As a result, the gambler's fallacy can also be attributed to the mistaken belief that gambling — or even chance itself — is a fair process that can correct itself in the event of streaks, otherwise known as the "just-world hypothesis."

Bogle's Issue with 'Revision to the Mean'

A mathematical concept (but not a law) that is closely related to the gambler's fallacy is 'reversion to the mean.' In this statistical sense, a gambler who expects to see average results grossly underestimates how large a sample size is needed for convergence to the average.

The late John Bogle, who founded the Vanguard Group, repeatedly pointed out this problem and received a great deal of criticism from the active management industry. This wasn't very suprising to IFA's advisors, though, since reversion to the mean statistically negates the possibility of skill being the explanation for an active manager beating his or her benchmark on a purely returns-based examination. 

Interestingly, one of Bogle's most vociferous critics, hedge fund manager Andrew Feinberg, had a change of heart when he was forced to explain his own lackluster performance in 2011. He was quoted by Kiplinger magazine as saying: "Mutual fund managers who beat the market for a time have a nasty habit of reverting to the mean."

At Index Fund Advisors, our approach incorporates the concept that securities prices change based on current news to ensure that the expected return of an investment remains the same in order to compensate investors for bearing the risk of that investment.

The law of large numbers can work to our advantage in two ways, or what we call double diversification. This can be accomplished by maximizing the number of securities held (asset diversification) and maximizing the number of days of market exposure (time diversification).

Regardless of how many anomalous periods we see of consecutive up or down days, we do not waiver from the most basic principle of every day having the same expected return. If there is a better approach to investing, we have yet to see it.

As IFA's Founder and CEO Mark Hebner explains in Step 11 of his book, Index Funds: The 12-Step Recovery Program for Active Investors, trying to completely avoid risk — as some might attempt to do — is futile. "Avoiding risks," he writes, "positions investors to avoid returns." 

---

This is not to be construed as an offer, solicitation, recommendation, or endorsement of any particular security, product or service. There is no guarantee investment strategies will be successful.  Investing involves risks, including possible loss of principal. Performance may contain both live and back-tested data. Data is provided for illustrative purposes only, it does not represent actual performance of any client portfolio or account and it should not be interpreted as an indication of such performance. IFA Index Portfolios are recommended based on time horizon and risk tolerance. Take the IFA Risk Capacity Survey (www.ifa.com/survey) to determine which portfolio captures the right mix of stock and bond funds best suited to you. For more information about Index Fund Advisors, Inc, please review our brochure at https://www.adviserinfo.sec.gov/ or visit www.ifa.com.