To financial historians and statisticians, William Sealy Gosset is referred to simply as "The Student." And with good reason. While working for the Guinness brewery in Ireland to evaluate the quality of ingredients used to make beer, he introduced in 1908 a mathematical experiment known as a "t-test."
Today, the t-test is being applied in modern finance to determine if a series of historical returns is reliably superior — i.e., showing a t-statistic of 2 or higher — to a risk-equivalent benchmark. This can determine whether alpha (any return above the benchmark return) is due to luck or skill.
How is it done? In calculating the t-stat, the first step is to determine the excess returns the manager earned above an appropriate benchmark. Then, we determine the regularity of the excess returns by calculating the standard deviation of those returns.
Based on these two numbers, we can calculate how many years we need to support the manager's claims.
For example, let's say that in a sample with 80 fund managers who had positive excess returns, the average excess return was 0.84% and the standard deviation was 5.64%.
To estimate the years needed for statistical significance, you can find the intersection of the average excess return (about 0.8%) and standard deviation (about 5.6%) in the chart below (see data box for point estimates). Then follow the line out, and you can see that 180 years of returns data are needed to establish skill as the reason for the higher returns.
Also worth noting: The calculator below the chart provides the exact number of years needed. Obviously, no manager has ever managed a fund for 180 years. Therefore, we are unable to accept any of these manager's claims. Alas, managers are mere mortals.
The figure below shows the formula to calculate the number of years needed for a t-stat of 2. We first determine the excess return over a benchmark (the alpha), then determine the regularity of the excess returns by calculating the standard deviation of those returns. Based on these two numbers, we can then calculate how many years we need (sample size) to support the manager's claim of skill.
As you see in the calculator above, the t-stat is held at 2. Understanding why a t-stat of 2 or more is considered statistically significant is important. However, it is vital to simply grasp why bigger t-stats mean the value is more "reliably" different from zero.
To begin with, refer to the following equation defining a t-stat:
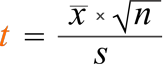
or t-stat = (average x √Observations ) / standard deviation
Decomposing the elements of this equation can demonstrate what leads to bigger t-stats and help instill the intuition behind why a bigger t-stat implies that the observed value is less likely to have a true value of zero.
"Average" is the average of all observations in the sample. This parameter is in the numerator, so as the average increases, so does the t-stat. To illustrate, consider the two data series below:
Series A: 1, 2, 1, 2, 1, 2, 1, 2, 1, 2
Series B: 9, 10, 9, 10, 9, 10, 9, 10, 9, 10
Both have the same number of observations and the same standard deviation. But series A has an average of 1.5 and series B has an average of 9.5. As the average increases, so does the t-stat, meaning it is less likely the true average from series B is actually zero.
The intuition here is that a mean further from zero makes it less likely that the true value is in fact zero.
"√N" is the square root of the number of observations. This parameter is also in the numerator, so as the number of observations increases, the t-stat does as well. Consider the two data series below:
Series A: 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2
Series B: 1, 2, 1, 2
Both have the same average of 1.5 and the same standard deviation of 0.5, but series A has 20 observations and series B only has 4. As the number of observations increases, so does the t-stat — and the observed average becomes more reliable. In this example, series A has a t-stat of 13.4 and series B has a t-stat of 6 due to the difference in the number of observations. This means series A is more reliably different from zero than series B.
The intuition here is that a larger number of observations results in more reliability.
"Standard deviation" is a measure of how much the individual observations in the sample vary from the average. This parameter is in the denominator, so as the standard deviation decreases, the t-stat increases. Consider the two data series below:
Series A: 9, 10, 9, 10, 9, 10, 9, 10, 9, 10
Series B: 18, 0, -18, 32, 10, -20, 40, 15, 8, 10
Both have the same 9.5 average and the same number of observations, but series A has much less volatility and a lower standard deviation than series B. As the standard deviation increases, the t-stat decreases, so the average from series B is less reliably different from zero than the same average from series A. Put differently, there is a greater likelihood the 9.5 average from series B happened by chance due to the volatility of the data series.
The intuition here is that a more volatile data series results in a mean that is less reliably different from zero. Here is a calculator to determine the t-stat. Don't trust an alpha or average return without one.
The Fama and French Risk Premiums are good examples of the use of the t-stat. Based on the long-term data, there has been an excess return for exposure to these risk factors, referred to as the U.S. Equity Premium (Risk of the Total Market - Risk Free - 30 d T-Bill), the U.S. Value Premium (High Book to Market - Low Book to Market), and the U.S. Size Premium (Small Companies - Big Companies).
An important consideration for investors is the likelihood that these risk "premiums" are actually zero (i.e., there is no premium) — despite a historical mean that is positive.
As discussed earlier in this piece, the starting point is calculating a t-stat for each return series as outlined in the bar charts below. The t-stats in the bar charts are all considered statistically significant (i.e., greater than 2), and we can almost be 99% sure that all three risk premiums are positive, with only the (S-B) t-stat being marginally lower than the required 2.6 for that level of significance.
All five data series have the same number of observations, so differences in their t-stats will be a function of different means and standard deviations.
As you can see, the equity premium is the most reliable — i.e., different from zero — despite having the highest volatility because it has a significantly higher mean to go with it. Conversely, the size premium is less reliable than the value premium despite having nearly the same volatility because it has a lower historical mean.
In "Challenge to Judgment," Nobel laureate economist Paul Samuelson dismisses investors who claim they can find benchmark-beating managers by saying, "They always claim that they know a man, a bank, or a fund that does do better. Alas, anecdotes are not science. And once Wharton School dissertations seek to quantify the performers, these have a tendency to evaporate into thin air—or, at least, into statistically insignificant t-statistics."
Although a few managers will occasionally appear to have reliably delivered alpha, IFA cautions investors that the fact that there are so many managers virtually guarantees that there will be some who appear to have demonstrated true skill. Unfortunately, the number of such managers is no higher than what we would have if all of them were monkeys throwing darts at the Wall Street Journal.
This is not to be construed as an offer, solicitation, recommendation, or endorsement of any particular security, product or service. There is no guarantee investment strategies will be successful. Investing involves risks, including possible loss of principal. IFA Index Portfolios are recommended based on time horizon and risk tolerance. Take the IFA Risk Capacity Survey (www.ifa.com/survey) to determine which portfolio captures the right mix of stock and bond funds best suited to you. For more information about Index Fund Advisors, Inc, please review our brochure at https://www.adviserinfo.sec.gov/